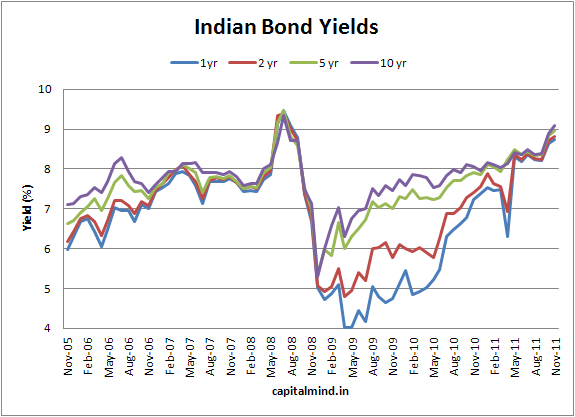
Data from CCIL shows that last Friday, the 10 year bond yield inched above 9%, which is inching towards the high of 9.35% set in July 08. (Note: that was just one month before it reversed)
The spreads are incredibly tight, but they’ve been that way earlier, in 07-08 as well. For yields to fall, there needs to be either a rate cut or a crisis (when people will run to the safety of government bonds).